ブリュアンゾーン

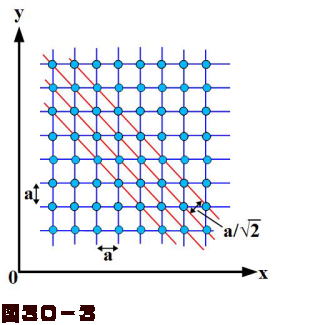
ブリユアンゾーン（英: Brillouin Zone、略称BZ）とは、逆格子におけるウィグナーザイツ胞のことである。ブリルアンゾーン、ブリユアン域とも言われる。

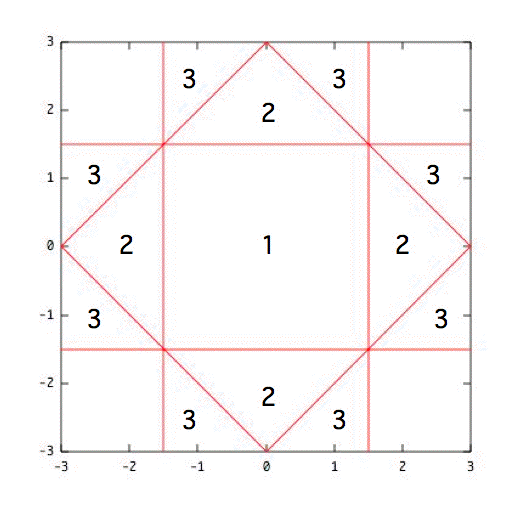
ある逆格子点の周りの逆格子点の垂直二等分面によって作られる領域は、無数にできるが、その中で最小の領域のことを第一ブリユアンゾーンという。それ以外は、第二ブリユアンゾーン、第三、、と称していく。

ブリュアンゾーンは固体物理学において、波の散乱による回折条件を表現するために広く用いられている。これは、電子のエネルギーバンド理論などの説明に便利である。たとえば波数ベクトルがブリュアンゾーン上にあるとき、電子波のブラッグ反射が起きる。

結晶内の電子とブリュアンゾーン

量子力学では、波動関数をψとし、Rを実空間での結晶内の適当な実格子ベクトルとすると、

${\displaystyle \psi _{\mathbf {k} }(\mathbf {r} \mathbf {R} )=e^{i\mathbf {k} \cdot \mathbf {R} }\psi _{\mathbf {k} }(\mathbf {r} )}$

が成り立つようなkが存在する。このkは波数ベクトルである（参照：ブロッホの定理）。

波数ベクトルkの集合を波数空間（k空間）と呼ぶ。また、任意の逆格子ベクトルGとRとは、

${\displaystyle e^{i\mathbf {G} \cdot \mathbf {R} }=1}$

という関係があるため、kとk Gは等価であり、これは第一ブリュアンゾーンのみを考えればよいことを意味する。

k点

ブリュアンゾーン内においてメッシュによって区分された各点(Sampling points)のことをk点（k-point）と呼ぶ。ブリュアンゾーン上のk点のうち、対称性の良い点に特に名称が付いており、X、L、Δ、Λ、Σなどの記号を付ける。ブリュアンゾーン内部はギリシャ文字で、表面はアルファベットで記す。

なお大文字のK点は、k点とは意味が異なり、対称性を表す記号Kのことを意味する。

関連項目

• 逆格子空間
• バンド理論
• バンド構造
• 第一原理バンド計算
• レオン・ブリルアン
• 波数
• 特殊点法