相関

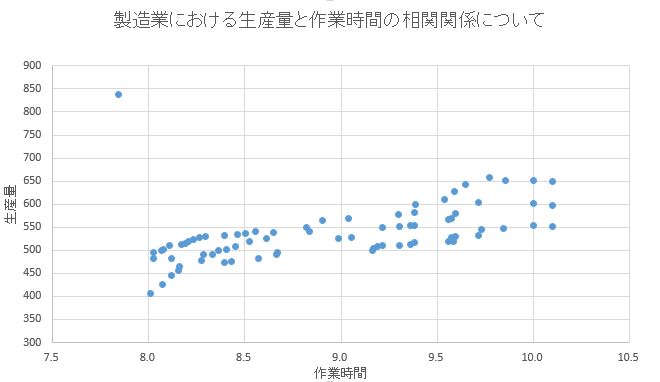
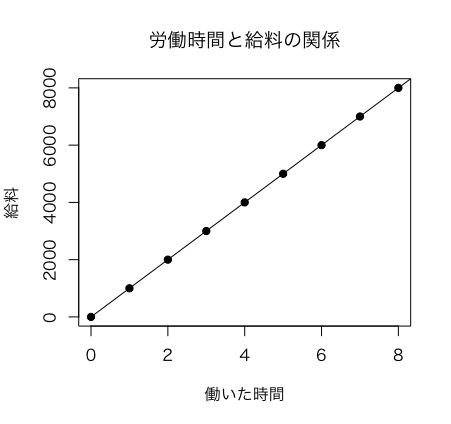
相関（そうかん、英: correlation）とは、一方が変化すれば他方も変化するように相互に関係しあうことである。数学や物理学では、二つの変量や現象がある程度相互に規則的に関係を保って変化することをいう。因果性の有無は問わない。広義には、統計的に何らかの関連性があることを言うが、最も一般的な相関係数であるピアソンの積率相関係数は二変数における線形性相関の程度を指す。例えば「親の身長が高いほうが子供の身長も高い」「勉強時間が長いほうがテストの成績も上がる」などの傾向が身近な相関現象である。

相関は、実践で活用できる予測的な関係性を示してくれるため実用性がある。例えば、電気事業者は電力需要と天候との相関関係に基づいて、過ごしやすい気温の日には電力を少なめに発電したりもする。この例では、猛暑や厳寒といった極端な天候は人々が大量に電気を使う原因となるため、因果関係にあたる。ただし一般には、相関があっても因果関係があるとは言い切れない（すなわち相関関係は因果関係を含意しない）。

本質的に相関とは、2つ以上の変数が互いにどの程度関わり合っているかの尺度である。幾種類かの相関係数があり、多くの場合${\displaystyle \rho }$または${\displaystyle r}$で表記される。統計学では、主に二変数の線形性相関に着目して関係性の強弱を係数で表しており、その最も一般的な尺度がピアソンの積率相関係数である（より堅牢なスピアマンの順位相関係数などは非線形相関にも対応する）。

ピアソンの積率相関係数

カール・ピアソンが考案した積率相関係数は、2変数間の相関を示す尺度として最もよく知られており、単に「相関係数」と言えば通常は「ピアソンの積率相関係数」を指す。数学的には、2変数の共分散を標準偏差の積で除算するだけで得られる。

ピアソンの相関係数は、実際のデータ群が期待値からどの程度外れているかを示すもので、-1から 1までの値で表される。データ群の変数間に何らかの線形的な関係性があれば、数値に正または負の符号がつき、無相関であれば値は0になる。

2つの確率変数を${\displaystyle X}$と${\displaystyle Y}$、各々の期待値を${\displaystyle \mu _{X}}$と${\displaystyle \mu _{Y}}$、そして標準偏差を${\displaystyle \sigma _{X}}$と${\displaystyle \sigma _{Y}}$とすると、母集団の相関係数${\displaystyle \rho _{X,Y}}$は次のように定義される。

ここでの${\displaystyle \operatorname {E} }$は期待値の作用素、${\displaystyle \operatorname {cov} }$は共分散を意味し、${\displaystyle \operatorname {corr} }$は相関係数の代替表記として広く使われている。ピアソン相関は、両方の標準偏差が有限かつ正の値である場合にのみ定義される。積率の観点から、次の式に書き改めたりもする。

対称性

この相関係数は対称性があり、${\displaystyle \operatorname {corr} (X,Y)=\operatorname {corr} (Y,X)}$である。これは乗算の可換性によって証明される。

積のような相関

確率変数${\displaystyle X}$と${\displaystyle Y}$の標準偏差を${\displaystyle \sigma _{X}>0}$と${\displaystyle \sigma _{Y}>0}$とすると、次のことが言える。

相関と独立

ピアソン相関係数の値は-1から 1の範囲をとり、完全な正の線形相関にあれば 1、完全な負の相関関係にあれば-1になる。それ以外の場合は-1から 1の範囲内にある何らかの値をとり、変数間における相関の強弱度合いを表す。値がゼロに近いほど関係性が乏しい（無相関に近い）ことになり、-1や 1に近いほど強い相関があることになる。

変数同士が独立 (確率論)である場合ピアソン相関係数は0となる。ただしピアソン相関係数は2変数間の線形相関のみを検出するため、この逆が真とは限らない。

例えば、確率変数${\displaystyle X}$が対称分布で${\displaystyle Y=X^{2}}$だとする。その場合${\displaystyle Y}$は完全に${\displaystyle X}$によって決定されるため${\displaystyle X}$と${\displaystyle Y}$は完全に従属だが、線形相関のみを検知するピアソン相関係数では0となる。同様に、ピアソン相関係数が 1や-1に近い値を示したからといって、必ずしも2変量に関係性があるとは限らない。偶然にも相関があるかのような 1や-1に近い係数になることがあり、これは疑似相関（見せかけの相関）と呼ばれる。なお、${\displaystyle X}$と${\displaystyle Y}$が正規分布という特殊なケースだと、無相関は独立と同義である。

無相関のデータが必ずしも独立を含むとは限らないが、相互情報量が0であれば確率変数が独立しているかどうかを確認可能である。

例

確率変数間の従属を表す別の尺度

ピアソンの積率相関係数によって与えられる情報だけでは、確率変数間の従属構造を定義するのに十分ではない 。この相関係数は、分布が多変量正規分布の場合など、非常に特殊な場合にのみ従属構造を完全に定義する。楕円分布の場合、それは等密度の楕円という特性を有する。ただし、従属構造を完全に特徴付けるわけではない。

距離相関 (Distance correlation) は、従属確率変数についてゼロになりうるというピアソン相関の欠陥に対処する目的で導入された。距離相関のゼロは独立性を意味する。

確率的依存係数(Randomized Dependence Coefficient,RDC) は、計算効率の良い多変量確率変数間のコピュラ (統計学)に基づく依存の尺度である。RDCは確率変数の非線形スケーリングに関して不変であり、関数に関連した幅広いパターンを発見可能であり、独立では値が0になる。

バイナリ変数2つの場合、オッズ比はその従属性を測るもので、数値が負になることはなく場合によっては無限大[0, infty]となる。ユールのY (Yule's Y) やユールのQなどの関連統計は、これを相関のような[-1, 1]の範囲に正規化している。オッズ比は、ロジスティック回帰モデルによって従属変数が離散かつ独立変数が1つ以上あっても構わないモデルケースに一般化されたものである。

相関比、エントロピーに基づく相互情報量、合計相関、二重合計相関、多分相関もまた全て、それらの間のコピュラを考慮することで、より一般的な依存関係を検出しうる機能がある。一方で決定係数は、相関係数を重回帰へと一般化する。

データ分布に対する感度

変数${\displaystyle X}$と${\displaystyle Y}$間の従属度合いは、その変数が表されるスケールに左右されない。つまり、${\displaystyle X}$と${\displaystyle Y}$間の関係性を分析している場合、大半の相関尺度は${\displaystyle X}$をa   bXへと${\displaystyle Y}$ をc   dYへと変換したところで影響を受けない（ここでのa, b, c, dは定数で、bとdは正値）。 これは、一部の相関統計ならびにその類似群にも当てはまる。順位相関係数など一部の相関統計は、 ${\displaystyle X}$や${\displaystyle Y}$の周辺分布の単調変換に対しても不変である。

大半の相関尺度は、${\displaystyle X}$と${\displaystyle Y}$が標本採集された手法に大きく反応する。（右図で例示されているように）より広い範囲で値を見たほうが従属関係は強くなる傾向がある。したがって、成人男性全員から父親と息子間における身長の相関係数を考えた場合と、父親の身長を165-170cmに絞った場合に算出される同様の相関係数と比較すると、後者の場合は相関が弱くなる筈である。一方または双方の変数における制限範囲を修正しようとする手法が幾つか開発されており、メタ解析で一般的に使用されている。最も一般的なものが、ソーンダイクによるケースIIとケースIIIの式である。

${\displaystyle X}$と${\displaystyle Y}$における特定の同時分布では、使われている様々な相関尺度が定義されない場合もある。例えば、ピアソンの積率相関係数は積率の観点から定義されるため、積率が未定義であれば定義できなくなる。分位数に基づく従属性の尺度は常に定義される。母集団の従属性尺度を推定することを目的とした標本ベースの統計には、データ採集された母集団の空間構造に基づく不偏性であったり漸近的な一貫性（一致性）があるなどの望ましい統計的特性を有する場合もあればそうでない場合もある。

データ分布に対する感度は有益に活用されている。例えば、スケール変換済みの相関 (scaled correlation) は時系列のうち短い期間での相関関係を拾い出す目的でその範囲への感度を調整するように工夫されたものである。規定された方法で値の範囲を縮めることにより、長期間スケールの相関が除外され、短期間スケールの相関のみが明らかとなる。

相関行列

${\displaystyle n}$の相関行列の確率変数${\displaystyle X_{1},\ldots ,X_{n}}$ は${\displaystyle n\times n}$の行列で、その成分${\displaystyle (i,j)}$は${\displaystyle \operatorname {corr} (X_{i},X_{j})}$である。したがって、対角成分はすべて等しく1である。 使用される相関の尺度が積率相関係数である場合、相関行列は標準化された確率変数${\displaystyle X_{i}/\sigma (X_{i})}$ for ${\displaystyle i=1,\dots ,n}$の共分散行列と同一である。これは母集団相関行列（その場合${\displaystyle \sigma }$は母集団標準偏差）と標本相関行列（この場合${\displaystyle \sigma }$ は標本標準偏差を示す）の両方に当てはまる。したがって、各々が半正定値行列である必要性がある。さらに、他の値の線形関数として全ての値を生み出せる変数がない場合、相関行列は厳密に正定値である。

${\displaystyle X_{i}}$と${\displaystyle X_{j}}$とが相関関係であり、${\displaystyle X_{j}}$と${\displaystyle X_{i}}$との相関も同じであるため、相関行列は対称である。

相関行列は、例えば重相関係数の場合1つの式の中に現れ、重回帰における適合度の尺度として表示される。

統計モデル構築において、変数間の関係を表す相関行列は異なる相関構造に分類され、推定に必要なパラメータの数などの要因によって区別される。例えば、確率変数が交換可能 (Exchangeable random variables) な相関行列では、変数同士のあらゆるペアが同じ相関を持つものとしてモデル構築されるため、行列の対角以外の成分は全て互いに等しくなる。一方、尺度は時間的に密接している場合に相関が大きくなりがちなので、変数が時系列を表す場合はしばしば自己回帰行列が使用される。

探索的データ解析の相関図 (Iconography of correlations) は相関行列を置き換えたダイアグラムで出来ており、そこでは「顕著な」相関が実線（正の相関）または点線（負の相関）で表されている。

最近傍相関行列

一部の応用(例えば、部分的に観測されたデータだけでデータモデルを構築する)において、相関を近似的に表す行列からそれに最も近い相関行列（例えば、計算方法が原因で通常は半正値の条件を満たさない行列）を見つけたい人もいる。

2002年、ニコラス・ハイアム はフロベニウス標準形を 用いて近傍(nearness)の概念を形式化し、ダイクストラ法を用いて最近傍相関行列を計算する方法を提示した。

これが主題への関心を巻き起こし、その後数年間で新たな理論的成果（例えば、因子構造を用いた近傍行列の算出）や数理上の成果（例えば、最近傍相関行列を算出するためにニュートン法を用いる）が得られた。

確率過程の無相関と独立

2つの確率過程${\displaystyle \left\{X_{t}\right\}_{t\in {\mathcal {T}}}}$と${\displaystyle \left\{Y_{t}\right\}_{t\in {\mathcal {T}}}}$についても同様である。仮に両者が独立しているのなら、無相関である。この命題の逆が真とは限らない。2変数が無相関だとしても、互いに独立していない場合がある。

よくある誤解

相関と因果

「相関関係は因果関係を含意しない」という慣例的な語句は、相関関係がそれ自体から変数同士の因果関係を推測するのには使えないという意味である。この語句を、相関関係が因果関係の可能性を示すことができないという意味で捉えてはならない。しかし、相関関係の根底にある原因は間接的であったり未知な可能性もあり、高い相関は因果関係が存在しない等号関係（トートロジー）とも重複しうる。それゆえ、2変数間の相関関係は因果関係を（どちら向きにも）確立するだけの十分条件とはならない。

子供の年齢と身長との相関関係はだいぶ因果関係が透明であるが、ヒトの気分と健康との相関関係はそこまでとはいえない。慣用句で「病は気から」とあるが、病気に罹る・罹らないは我々の気分次第なのか？ 健やかな気分は健康をもたらすのか？ 健康は健やかな気分をもたらすのか？ 何か別の要因が両者の根底にあるのではないか？。 相関関係を因果関係の証拠として採用することは可能だが、どんな相関関係があったとしても因果関係が何であるかを示すことはできない。

単純な線形相関

ピアソンの積率相関係数は2変数間の線形関係の強さを示すが、一般にその値は両者の関係を完全に特徴付けるものではない。特に、${\displaystyle Y}$の条件付期待値を${\displaystyle X}$と置いた場合、示された${\displaystyle \operatorname {E} (Y\mid X)}$が${\displaystyle X}$内の線形ではないため、相関係数が完全には${\displaystyle \operatorname {E} (Y\mid X)}$の形に定まらない。

右の図はフランシス・アンスコムによる同一変数の散布図4組 (Anscombe's quartet) を示している。各${\displaystyle y}$変数はどれも同じ平均(7.5)、分散(4.12)、相関(0.816)および回帰直線(y = 3 0.5x)を有する。しかし、散布図で見られるようにその変数分布は大きく異なる。

左上は正常分布しているように見え、相関があって正規性の仮定に従う2変数を考えた場合に期待される事象に対応しているように思える。右上 は正常分布とは異なるもので、2変数間の明らかな関係性は観察できるが線形ではない。この場合、ピアソン相関係数は厳密な関数的関係の存在を示すことはできず、その関係を線形関係で近似したものを示すに過ぎなくなる。左下では、相関係数を1から0.816に下げてしまうのに十分な影響を及ぼす外れ値1つを除けば、線形関係は完全である。最後の右下は、2変数間の関係が線形でないにもかかわらず、1つの外れ値が高い相関係数を生成するのに十分な例を示したものである。

これらの例は、相関係数が要約統計量 (Summary statistics) としてデータ可視化による検討の代替にならないことを示すものである。これらの例は、ピアソン相関がデータが正規分布に従うことを前提にしていることを示すものと言わたりもするが、これは部分的に正しいに過ぎない。ピアソン相関は、実際に遭遇したほとんどの分布を含む有限共分散行列を持つ分布について正確に計算することができる。ただし、ピアソン相関係数（サンプル平均値および分散値と一緒に取得）は多変量正規分布からデータが引き出された場合に十分統計量となるに過ぎないのである。その結果、ピアソン相関係数は多変量正規分布からデータが引き出された場合にのみ、変数間の関係を完全に特徴付けることになる。

2変量正規分布

2つの確率変数${\displaystyle (X,Y)}$が2変量正規分布に従う場合、条件付き平均${\displaystyle \operatorname {E} (X\mid Y)}$は${\displaystyle Y}$,の線形関数である。${\displaystyle X}$と${\displaystyle Y}$間の相関係数${\displaystyle \rho _{X,Y}}$は、周辺平均および${\displaystyle X}$と${\displaystyle Y}$の分散とともに、この線形関係を決定している。

${\displaystyle \operatorname {E} (Y\mid X)=\operatorname {E} (Y) \rho _{X,Y}\cdot \sigma _{Y}{\frac {X-\operatorname {E} (X)}{\sigma _{X}}},}$

ここで${\displaystyle \operatorname {E} (X)}$と${\displaystyle \operatorname {E} (Y)}$はそれぞれ${\displaystyle X}$と${\displaystyle Y}$の期待値で、${\displaystyle \sigma _{X}}$と${\displaystyle \sigma _{Y}}$はそれぞれ${\displaystyle X}$と${\displaystyle Y}$の標準偏差である。

経験的相関${\displaystyle r}$は、相関係数${\displaystyle \rho }$の推定量である。${\displaystyle \rho }$の分布推定量は、以下の式にて求められる。 $${\displaystyle \pi (\rho |r)={\frac {\Gamma (\nu 1)}{{\sqrt {2\pi }}\Gamma (\nu {\frac {1}{2}})}}(1-r^{2})^{\frac {\nu -1}{2}}\cdot (1-\rho ^{2})^{\frac {\nu -2}{2}}\cdot (1-r\rho )^{\frac {1-2\nu }{2}}F\!\left({\frac {3}{2}},-{\frac {1}{2}};\nu {\frac {1}{2}};{\frac {1 r\rho }{2}}\right)}$$

ここで${\displaystyle F}$はガウスの超幾何関数であり${\displaystyle \nu =N-1>1}$となる。この密度がベイズの事後密度であり、正確な最適信頼分布密度でもある。

標準誤差

${\displaystyle x}$と${\displaystyle y}$が確率変数の場合、標準誤差は次の相関と関連性がある。

${\displaystyle SE_{r}={\frac {1-r^{2}}{\sqrt {(n-2)}}}}$

ここで${\displaystyle r}$は相関、${\displaystyle n}$は標本数である。

関連項目

• 自己相関
• カノニカル相関
• 決定係数
• 共和分
• 相関関数
• 相関係数
• 共分散
• 相互相関関数
• 錯誤相関
• 擬似相関

脚注

注釈

出典

外部リンク

• 統計WEB「統計学の時間」-26章「相関分析」
• 内閣府統計局「統計学習の指導のために」-総合学習のための補助教材
• MathWorld page on the (cross-)correlation coefficient/s of a sample
• Proof that the Sample Bivariate Correlation has limits plus or minus 1
• Interactive Flash simulation on the correlation of two normally distributed variables by Juha Puranen.