計算量理論において、最小のクリーク被覆(クリークひふく、英: clique cover)を求めることは、グラフ理論的NP完全問題である。クリーク被覆問題はリチャード・カープによるオリジナルの21問題の1つで、そのNP完全性は1972年の論文 "Reducibility Among Combinatorial Problems"(「組合せ論的問題間の還元可能性」)に示されている。
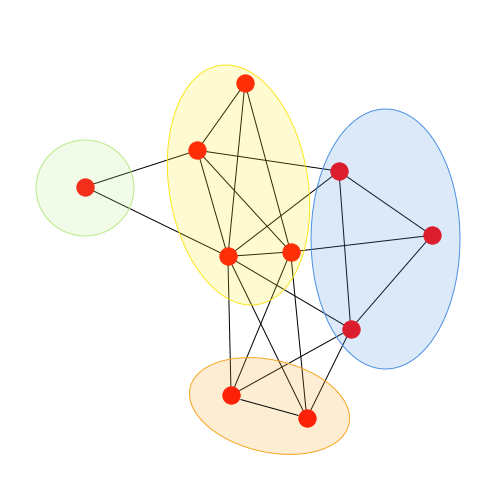
クリーク被覆問題(クリーク分割問題と呼ぶこともある)とは、与えられたグラフの頂点集合を k-個のクリークへ分割できるかを決定する問題である。頂点集合の k-個の集合への分割が与えられたとき、その各集合がクリークを成すかは多項式時間で判定することができるから、クリーク被覆問題はNPに属する。そのNP完全性はグラフの k-彩色可能性からの帰着である。これを見るには、まずグラフ G の k-彩色可能性をその補グラフ G′ に関する事実に翻訳すればよい。このとき G の k-個のクリークへの分割は G′ の k-個の独立集合への分割を求めることに対応する(各集合にそれぞれ別の1つの色を塗ることで k-彩色ができたことになる)。
この問題と関連して、クリーク辺被覆問題は与えられたグラフの辺をすべて含むようなクリークの集合を考えるもので、これもまたNP完全問題である。
参考文献
- Karp, Richard (1972), “Reducibility Among Combinatorial Problems”, in Miller, R. E.; Thatcher, J. W., Proceedings of a Symposium on the Complexity of Computer Computations, Plenum Press, pp. 85–103, http://www.cs.berkeley.edu/~luca/cs172/karp.pdf 2008年8月29日閲覧。
- Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 0-7167-1045-5 A1.2: GT19, pg.194.


.jpg)